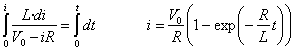SERGIO ALEJANDRO AMORTEGUI GONZALEZ
UNIVERSIDAD CENTRAL
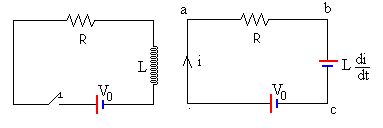
En el campo de la Ingeniería electrónica, las integrales cumplen una función muy importante, para calcular corrientes, capacitancias, tiempos de carga y descarga de corriente, entre otras. Pero fundamentalmente, el cálculo integral es utilizado en circuitos RLC (resistencia, condensador y bobina) para analizar su comportamiento dentro del circuito, por ejemplo:
- Para calcular el flujo de electrones por un conductor a través del tiempo, se emplea la siguiente ecuación:
q(t)=∫i(t) dt (Siendo (q)= carga; (i) corriente) desde un tiempo t1 a t2
- Cuando queremos averiguar la energía que posee un circuito, basta con integrar la potencia del circuito de un tiempo (t1) a un tiempo (t2) de la siguiente manera:
w(t)=∫p(t) dt (Siendo W= energía; p= potencia) desde un tiempo t1 a t2
- Para averiguar el voltaje en un condensador en un tiempo determinado se tiene:
vc(t)=1/c∫ic(t) dt (Siendo Vc= voltaje en el condensador; C= valor del condensador,Ic= corriente en el condensador) con respecto al tiempo (t)
desde un tiempo t1 a t2
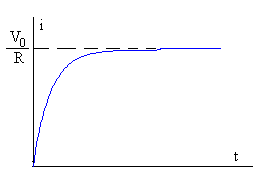
- Si queremos averiguar la corriente en una bobina o inductor en un tiempo determinado se tiene:
iL(t)=1/L∫vL(t) dt desde un tiempo t1 a t2
(Siendo IL= corriente en la bobina L= valor de la bobina en (mH); VL= voltaje en el inductor) con respecto al tiempo (t)
- Cuando se quiere hallar potencia a partir de un valor de resistencia y una corriente determinada, basta con hallar la integral del producto entre la resistencia por la corriente al cuadrado, así:
W(t)=∫Ri²(t) dt desde un tiempo t1 a t2
(Siendo W (t)= potencia en el tiempo,R= resistencia en Ohmios, I= corriente en amperios).
Esta es una pequeña muestra de la gran importancia que tienen las integrales en la ingeniería electrónica. Esto sin contar el cálculo de volúmenes que son fundamentales para calcular el núcleo de un transformador, para estimar el campo magnético producido. O las series y sucesiones que son importantes para estimar las dimensiones de una señal o pulso eléctrico, medido con el osciloscopio.
![]() .
.![]()
![]()
![]()
![]()
![]()